Ambient And Directional Lighting In Spherical Harmonics
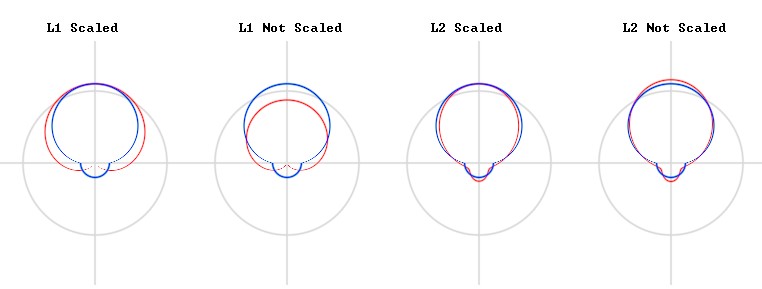
Stupid SH Tricks by Peter-Pike Sloan, released in 2008, is an excellent reference on spherical harmonics (SH). It covers many techniques for representing lighting as SH, including:
- Scaling SH for a directional light so that it matches when the normal exactly faces the light
- Extracting an ambient and directional light from environment lighting represented as SH
Extracting lighting from SH has different solutions depending on how you choose to represent your directional lights and whether you are working with L1 (4-term) or L2 (9-term) SH. This post works through the derivation for all these cases, hopefully improving clarity for anyone looking to implement it, and a shadertoy that demonstrates the results.